1 引言
三电平逆变器中电容电压的平衡问题是保证电机安全高效运行的一个重要标志，若三电平逆变器的直流侧电容电压得不到平衡，结果会使输出电压包含二次或更高次的偶次谐波，这对交流传动装置会造成极大的破坏。所以中点电位漂移是三电平逆变器必须要解决的问题。本文采用基于d-q坐标系的三电平svpwm算法来完成三电平系统主算法的实现，并在此基础之上，提出两种中点平衡控制策略来解决中点平衡问题，并对两种算法做比较分析。
2 基于d-q坐标系算法的实现
三电平逆变器共有27个基本矢量可供选择，整个空间电压矢量分布图可以划分为6个扇区共24个三角形区域（见图1）。 参考电压矢量所处的扇区位置可根据参考电压矢量的角度来确定。如图2所示，将任意一个60°扇区划分a、b、c、d四个小三角形。当某一长度的参考矢量v＊在某一扇区内旋转时有可能会跨越不同的三角形区域，据此将矢量工作模式划分为a模式、ac模式、bcd模式和bd四种。在不同区域的临界处存在着矢量切换角，如图2所示，θ1、θ2可通过简单的三角运算获得，这样通过矢量切换角θ1、θ2就可以清晰的确定参考矢量所在的三角形区域，根据ntv（the nearest triangle vectors）原则，用构成该三角形的三个固有矢量来合成该参考矢量，这样各个矢量的作用时间便可以获得，在不同的三角形区域内各个矢量的作用时间如图3所示。
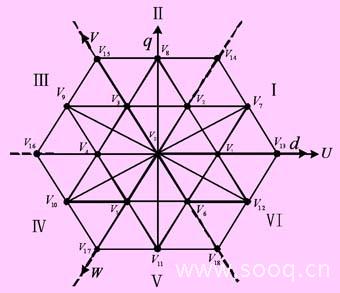
图1 三电平逆变器空间电压矢量图
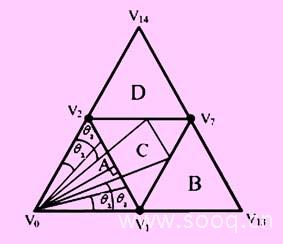
图 2 矢量切换角示意图
.jpg)
图 3 矢量作用时间分配图
3 中点电位平衡控制
3.1 基于控制因子m的滞环比较法
对电流方向做如下定义：流入负载中性点n的方向为负载电流正方向，流出直流侧中点的方向为中点电流的正方向。在27个电压矢量中只有18个矢量会影响中点电位，而这18个矢量作用的任意时刻，流入（或流出）中点电流的绝对值一定等于某相电流的ix（x=a，b，c）的绝对值。对于小矢量而言，当该相负载电流与直流侧中点直接相连时，定义此时的小矢量为正小矢量，中点电流i0=ix；当该相负载电流不与中点直接相连时，定义此时的小矢量为负小矢量，中点电流i0=-ix。对于中矢量而言，必然有i0=ix。设某一矢量的开关状态为（a，b，c），其中a，b，c=1，0，-1，则中点电流与负载电流关系可以综合为下式：
i0=ia（a+1）（1-a）+ib（b+1）（1-b）+ic（c+1）（1-c） （1）
在同样的负载状况下，一对正、负小矢量对中点电位的影响是完全相反的，所以适当的分配这两个矢量的作用时间就可以控制中点的漂移，这就是此种中点平衡策略的核心思想。
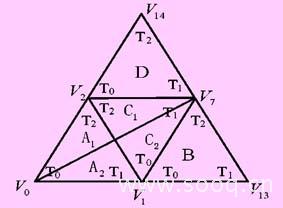
图4 滞环比较法矢量区域划分及矢量作用时间分配
以第一扇区为例，如图4所示，为了增强一对正、负小矢量对中点电位的调控能力，在三角形a1、c1、d中使用
这组小矢量；在三角形a2、c2、b中使用
小矢量。当矢量位于c1区时，如图中所示，此时小矢量v2的作用时间为t2，定义控制因子m（m∈（0,1）），设负小矢量的作用时间t2-=mt2，正小矢量作用时间t2+=（1-m）t2，定义中点电位的偏移量δv=vc2-vdc/2，其中vc2是下臂电容c2的电压， vdc是直流母线电压。基于以上定义，具体的调控则如下：
（1） 当δv>0，i0>0或δv<0，i0<0即δvi0>0时，增加该组负小矢量的作用时间，即保持m∈（0.5,1）；
（2） 当δv>0，i0<0或δv<0，i0>0即δvi0<0时，增加该组正小矢量作用时间，即保持m∈[0,0.5>；
（3） 当δvi0=0时，m=0.5。
3.2 基于控制因子ms0的准确计算法
实际上，中点电位漂移的根本原因是在一个开关周期内流入或流出中点的电荷不守恒，基于这一思想，如果能够保证每一个开关周期内流入中点的总电荷为零，就必然可以实现中点电位的精准控制，或者说将中点电位的波动降到最小。为简单起见，继续沿用上一方法的pwm输出序列规则。观察附表可以发现，在每一个周期中，脉冲序列总是以某一个小矢量的负小矢量（或正小矢量）开头并以该小矢量的负小矢量（或正小矢量）结尾，为了便于后文说明问题，称这一小矢量为主控小矢量；在一个pwm周期内除了主控小矢量以外，在某些区域还会用到相邻的小矢量，称为辅控小矢量。如图5所示，（0°,30°>区域的主控小矢量为v1，辅控小矢量为v2； （30°,60°>的主控小矢量为v2，辅控小矢量为v1。有关中矢量和大矢量的定义无任何变化。设某段区域的主控小矢量作用时间为tms0，辅控小矢量作用时间为 ，中矢量作用时间为tm，引入主控小矢量的时间分配系数ms0（ms0∈[-1,1>），并定义正小矢量的作用时间为tms0+=（1+ms0）tms0/2，负小矢量的作用时间为tms0-=（1-ms0）tms0/2，则正、负小矢量流入中点的总电荷为qms0=tms0+ix0-tms0-ix0=ms0ix0tms0，其中ix0代表与该小矢量相对应的某相电流即ix0=（ia，ib，ic）；进一步观察表1可以得到相邻小矢量流入中点的电荷为：qms=-ix1tms1，其中ix1代表与该相邻小矢量相对应的某相电流ix1=（ia，ib，ic）；中矢量流入中点的电荷为：qm=imtm；大矢量对中点电位无影响。如果要保证中点电位不发生波动，则必须保证流入中点的总电荷为零：qms0 +qms1+qm=0即:
ms0ix0tms0-ix1tms1+imtm=0 （2）
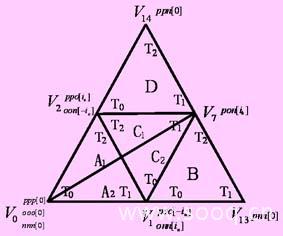
图5 包含中点电流大小和方向的矢量区域划分和作用时间分配
由于ms0∈[-1,1>，所以对解出的ms0应加以限定：当ms0＞1，取ms0=1，当ms0＜-1，取ms0=-1，这样就可以最大限度的发挥正负小矢量对中点电位的平衡能力。此种算法的缺陷是一旦中点出现偏移便不具有将中点电位拉回平衡点的能力的，为了弥补这一缺点，可以将第一种方法与本方法结合起来，具体实现如下：设定一个电压误差滞环δuset，如果中点电位的实际偏差δu<δuset，采用第二种方法；如果中点电位的实际偏差δu>δuset，采用第一种方法，这样就可以实现中点电位的准确控制。
4 仿真及结果分析
针对该算法，系统仿真参数设置如下：选用三相异步鼠笼电机，额定功率pn=4kw，额定线电压un=400v，额定频率fn=50hz，额定转速ωr=1430r/min，定子电阻rs=1.405ω，转子电阻rr=1.395ω，定子漏感lsl=0.005839h，转子漏感lrl=0.005839h，定转子互感lm=0.1722h，转动惯量j=0.0131kg.m2，极对数p=2，开关频率f=10khz，直流母线电压vdc=600v，直流侧电容c1=c2=1200μf，磁链幅值给定|ψs＊|=0.8wb。
4.1 采用基于控制因子m的滞环中点控制策略
为了验证该算法，现将系统的运行状态设定如下：t=0s时给定转速ωr=1200rpm＝125.6rad/s，空载启动，在t=0.2s时，突加负载转矩tl=15n·m。图6、7为此种控制策略下所得的波形。
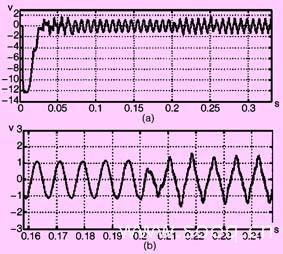
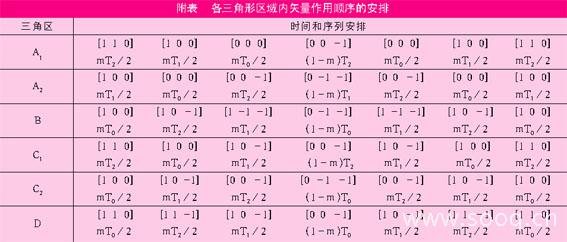
图6 直流侧下部电容电压与理想电压的偏差：vc2-vdc/2 （基于控制因子m）
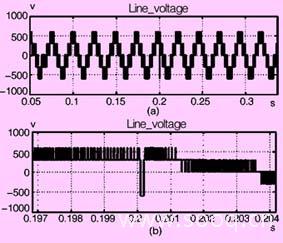
图7 线电压波形（基于控制因子m）
4.2 采用基于控制因子ms0的准确计算法中点控制策略
系统运行状态设定：t=0s时给定转速ωr=700rpm＝73.3rad/s，空载启动，在t=0.15s时，给定转速ωr=1200rpm＝125.6rad/s，t=0.24s时突加负载转矩tl=15n·m。偏差电压滞环设定值δu=1v。图8、9为此种控制策略的波形。
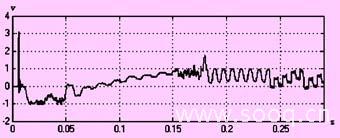
图8 直流侧下部电容电压与理想电压的偏差：vc2-vdc/2 （基于控制因子ms0）
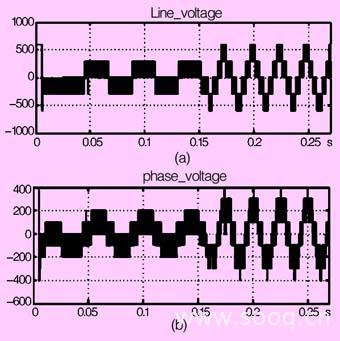
图9 线电压和相电压波形（基于控制因子ms0）
5 两种中点控制策略的比较
第一种中点控制方法的思想非常简单，由于采用滞环比较，所以它不可能在数量上对中点电位做出精确的补偿，或者说他并没有充分发挥正负小矢量对中点电位的补偿作用。基于控制因子ms0的平衡策略其计算量要远远大于基于控制因子m的平衡策略，而这种代价换来的就是中点电位控制精度的提高，通过设定偏差电压的滞环宽度，就可以将中点漂移限定在一定范围以内而不会受负载变化的影响，这也正是基于控制因子m的策略所不能做到的。至于这两种控制策略究竟选取哪一种，最终要视系统精度而定。
